Papers

Answer set programming (ASP) is the powerhouse technology you’ve never heard of

Formal Methods, PapersLeave a comment

The first person to explain answer set programming (ASP, pronounced ‘ay ess pee’) to me (Joe Osborn) told me about the three line implementation of graph coloring and the termination guarantees. Like any PL person, I recoiled in horror: you have an always-terminating language where I can solve NP-complete problems in three lines? So every time I write a program of three lines or more, I have to wonder… how exponential is this? No thank you!

I was wrong. Answer set programming is fast and easy to use; it’s a cousin to SAT that offers different tradeoffs than SMT, and I think PL folks have a lot to gain from ASP. As some evidence in that direction, let me tell you about an upcoming paper of mine appearing at POPL 2023, with Aaron Bembenek and Steve Chong.

From SMT to ASP: Solver-Based Approaches to Solving Datalog Synthesis-as-Rule-Selection Problems
Aaron Bembenek, Michael Greenberg, and Stephen Chong (POPL 2023)

https://greenberg.science/papers/2023popl_asp.pdf (artifact https://zenodo.org/record/7150677)

Datalog synthesis-as-rule-selection

Our paper is, on the face of it, about a program synthesis problem for Datalog: given a collection of candidate rules and an input/output example, select the candidate rules that transform the input to the output. The previous state-of-the-art (ProSynth) used a CEGIS loop: use Z3 to guess some rules, try it in Soufflé, use why- and why-not provenance to feed information back to Z3 to make a better guess. Our work gives three new solutions to the problem:

  • Datalog as a monotonic theory in SMT. Monotonic theories get a big performance boost, and modern solvers like Z3 and CVC4 support them. And Datalog is the monotonic theory ne plus ultra: we [read: Aaron] wrote Z3 and CVC4 plugins that turn any Datalog program into a monotonic theory. You can use this to do the CEGIS loop with a single call to SAT (but many calls to Datalog).
  • Using loop formulae to force SMT to find a least stable model. Every Datalog program has a logical denotation as the least model satisfying its Clark completion. Borrowing from ASP implementation techniques, we can use the Clark completion extended with loop formulae to rule out the hallucinatory models SMT is prone to finding. You can use this approach to do the CEGIS loop with not so many calls to Datalog, but possibly many calls to SAT.
  • Just encode it in ASP. The conventional ASP implementation strategy (grounder and solver) found in tools like clingo admits a direct encoding of the synthesis problem; our translator is just 187 SLOC. ASP lets you name that tune in just one note: you call the grounder, then you call the solver, and then you’re done.

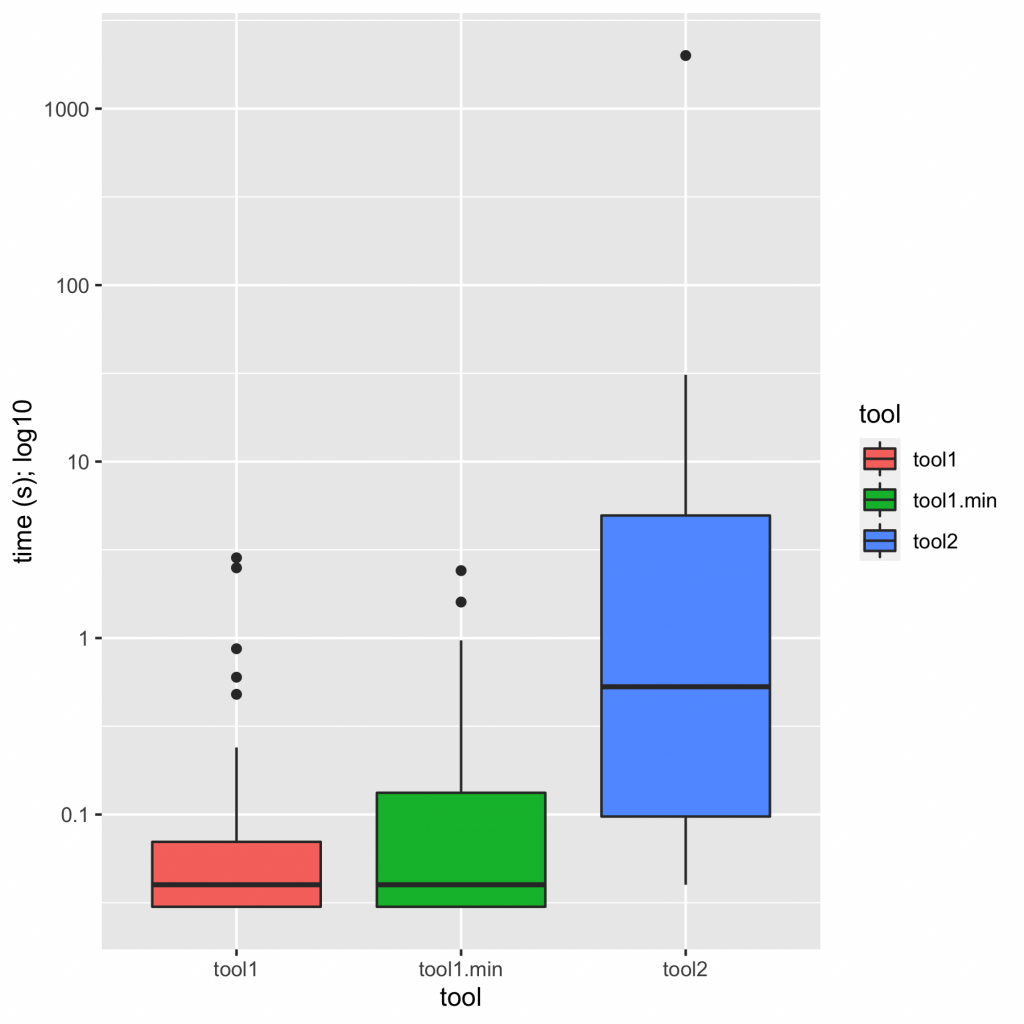
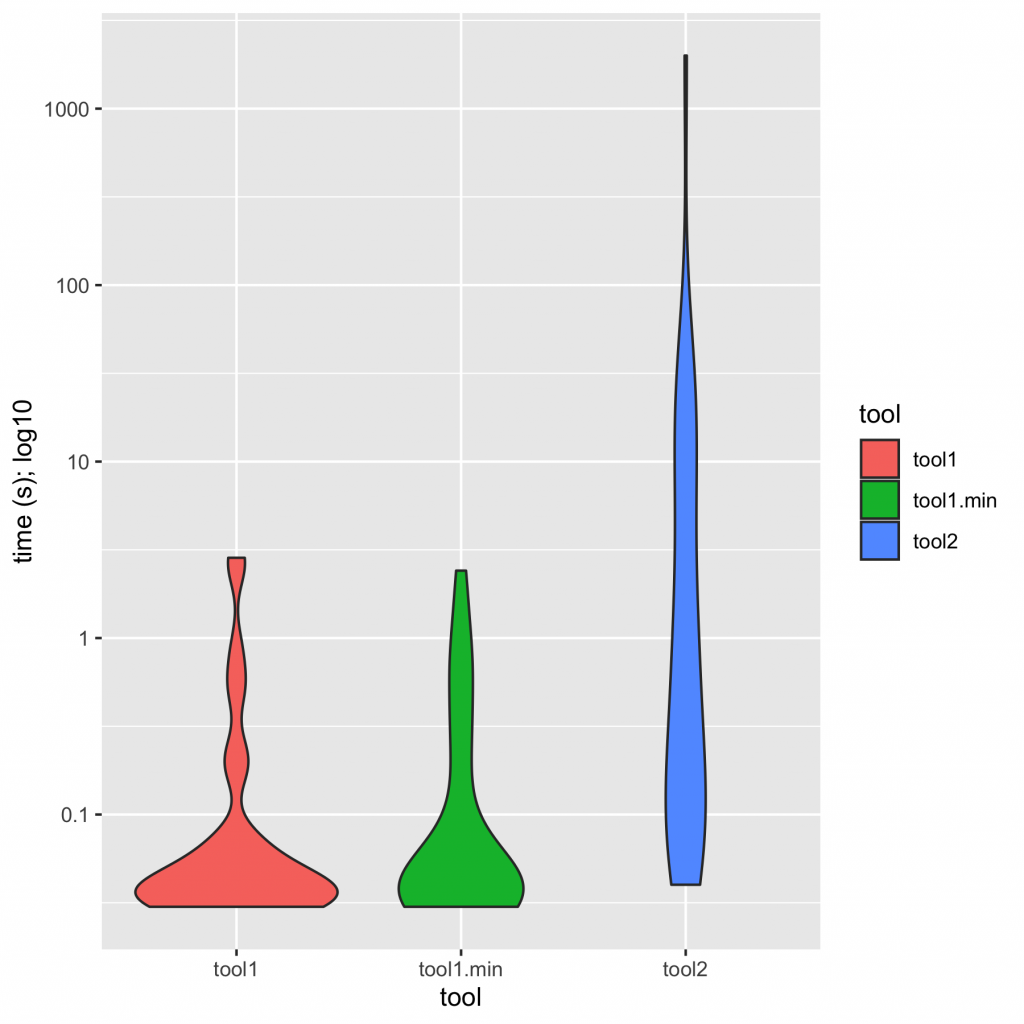
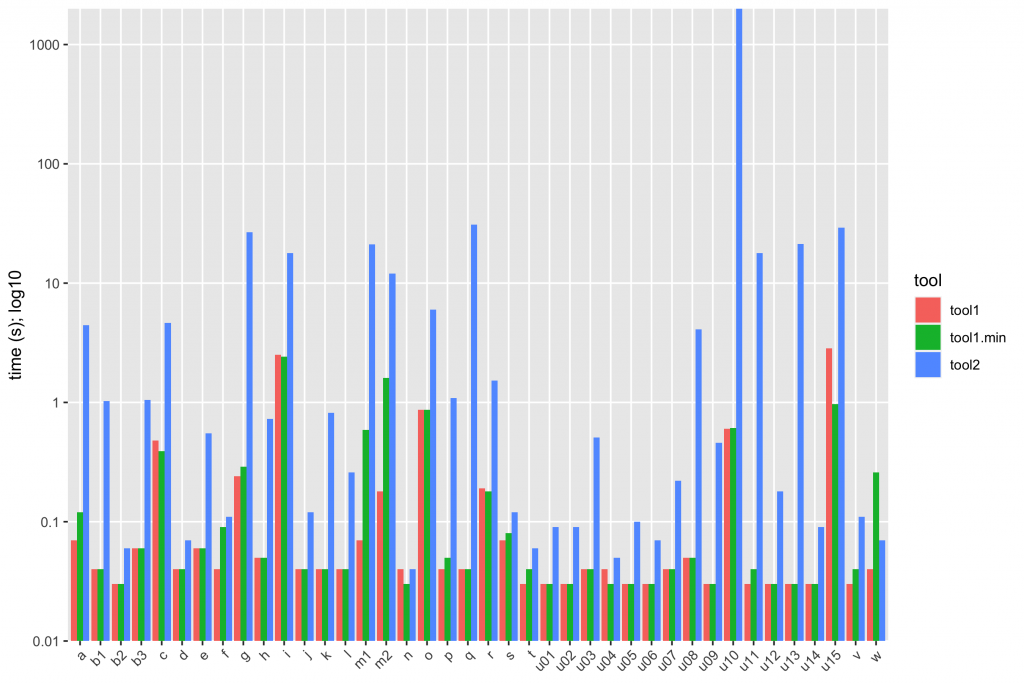
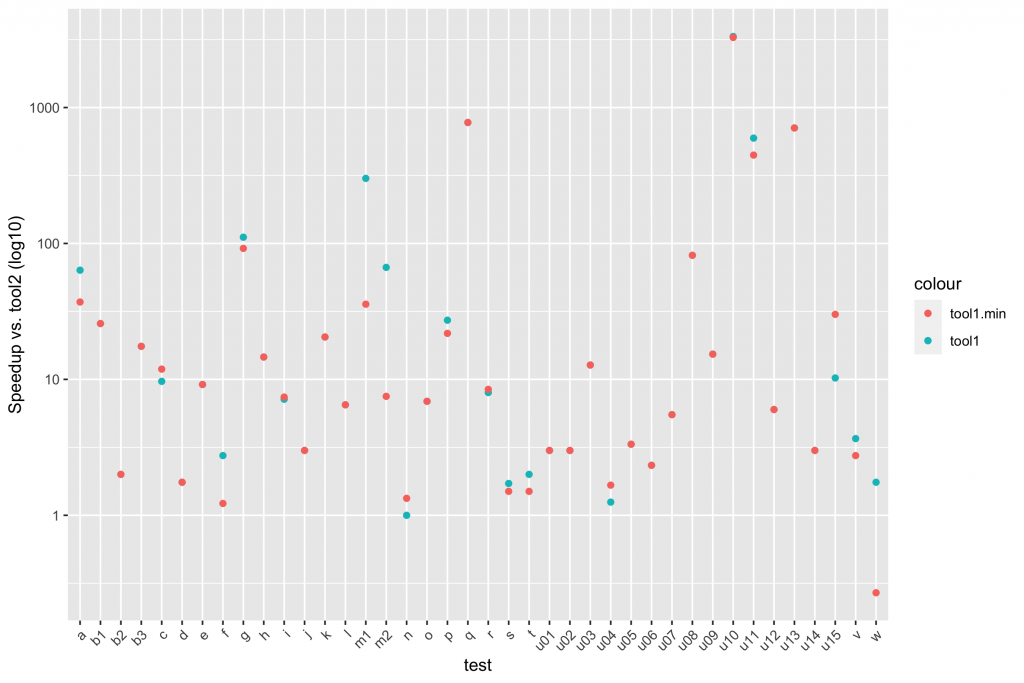
The gist of it is that the ASP solution is not only vastly simpler than the others, it outstrips them in performance, showing a ~9x geomean speedup compared to the state of the art. (I wrote previously about how to summarize early versions of these numbers.) Practically speaking, the ASP synthesizer always returns in under a second, while every other solution shows slowdowns on some of the benchmarks, taking tens of seconds or even timing out at ten minutes. There’s lots more detail in the paper.

I should add that the existing benchmarks are pretty easy: the examples are small, with example facts and candidate rules numbering in the low hundreds. In this setting, anything more than a few seconds isn’t worthwhile. We have some more criticism of the problem setting in the paper, but I can sum up my feeling as: when confronted with the benchmark challenge of implementing strongly connected components (SCC) in Datalog, who has the technical capacity to (a) write up an input/output example for SCC for a non-trivial graph, (b) generate several hundred candidate rules, (c) install and run a program synthesis tool, and (d) verify that the resulting program generalizes but (e) lacks the technical capacity to simply implement SCC in Datalog? Transitive closure is the “Hello World” of Datalog; strongly connected components is the “Fahrenheit-to-Celsius” of Datalog. The benchmarks don’t characterize a problem that anyone needs to solve.

Answer Set Programming

While I’m proud of the contributions outlined above, I’m most excited about introducing ASP to a broader audience. It’s a historical accident that ASP is more or less confined to the AI subfield, where a lot of great SAT and SMT research continues apace—not to mention the program synthesis work published at venues like AAAI and IJCAI under the umbrella of ‘inductive logic programming’. (Any PL person working on synthesis should look closely at Popper and ILASP.)

Our paper goes into more detail, but I like to contrast ASP with SMT by talking about justification. ASP will find solutions that are in some sense well justified by your problem statement (formally, it will find stable models); SMT has no such guarantee.

SMT solvers do an incredible job of finding witnesses for existentials: just (declare-const x Foo) and SMT will find your Foo, no problem. Well, maybe a problem: SMT’s approach to finding an x of type Foo is to go into the desert on a vision quest—it’ll keep hallucinating new values for x until it finds a satisfying one. On the plus side, that means SMT can find an x that doesn’t appear anywhere in the constraints you gave it. On the minus side, that means SMT is straight up hallucinating values—and you’re the one controlling set and setting to make sure SMT stays this side of sanity.

ASP never hallucinates. If something is in an answer set, it’s there for a reason. ASP’s non-monotonic semantics lets you freely mix negation and recursion (unlike Datalog, which forces negation to be stratified); the stable model semantics guarantees you won’t get nonsensical, circular answers that justify their premises with their conclusions.

Put simply: ASP is a SAT-like discipline that lets you work efficiently and correctly with inference rules. SMT is a SAT-like discipline that lets you work efficiently and correctly with existentials over equality and theory predicates. PL work needs both styles of reasoning; as we’ve shown, ASP can bring simple solutions and startling efficiency over complex appoaches using SMT. Maybe it’ll work for your problem, too?

How to cook a KAT for your pet theory

Networking, Papers, Programming Languages, Software, Temporal Logic and VerificationLeave a comment

Kleene algebra with tests is a beautiful, powerful framework for reasoning about programs. You can easily encode conventional While programs into KAT, and KAT enjoys decidable equality. Reasoning with KAT feels like you’re cheating Alan Turing himself: here we are, deciding nontrivial properties of programs!

The gist of KAT is that you write programs using a regular expression like notation: + for parallel composition, ; for sequential, and * for iteration. So you might encode:

while x > 0:
  y += 1
  x -= 1

As (xGt0; incY; decX)*; ¬xGt0, where xGt0 is a ‘test’ and incY and decX are ‘actions’. KAT’s equivalence decision procedure can prove that this program is equivalent to any finite unrolling of itself… neat!

NetKAT is the most impactful application of KAT: it’s an influential and successful academic project, and its ideas can already be found in numerous real, production systems. In light of NetKAT’s remarkable success… why don’t we apply KAT more often?

What’s hard about KAT?

On its own, KAT proves plenty of nice theorems, but none of them reason about particular program behaviors. In the code snippet above, xGt0, incY, and decX are uninterpreted—there’s no relationship between, say xGt0 and decX. That is, you might expect that ¬xGt0;decX;¬xGt0 is equivalent to ¬xGt0;decX, because decrementing a number less than or equal to 0 will yield a number that is also less than or equal to 0. The names of our tests and actions are suggestive, but KAT treats them absractly. If you want to reason about the semantics of your tests and actions, you need to build a custom, concrete KAT. NetKAT reasons about fields on packets, and doing so means building a particular, concrete KAT with particular actions. The original paper spends quite a bit of effort proving this new, custom KAT has a sound, complete, and decidable equivalence checking.

Worse still, KAT’s metatheory is very challenging. To create NetKAT, Nate Foster and company worked through closely related ideas for a few years before Nate joined Cornell and started working with Dexter Kozen, KAT’s progenitor. Only then did they realize that KAT would be a good fit, and they got to work on developing a concrete KAT—NetKAT. Unfortunately, “collaborate with Dexter” is an approach that doesn’t scale.

How to cook a KAT

In an upcoming PLDI 2022 paper, “Kleene Algebra Modulo Theories: A Framework for Concrete KATs”, Ryan Beckett, Eric Campbell, and I show how to generate a KAT over a given theory, i.e., a set of tests, actions, and their equational theory. We call the approach Kleene algebra modulo theories, or KMT. The paper covers quite a few examples:

  • booleans and bit vectors
  • monotonic natural numbers
  • unbounded sets and maps
  • NetKAT

What’s more, our approach allows for higher-order theories, like taking the product of two theories or using finite-time LTL to reason about another theory. (Our approach abstracts and generalizes Temporal NetKAT, which is just a concrete instance of our more general method.)

To build a KMT, you provide primitive tests and actions, along with weakest preconditions relating each pair of test and action. There’s an ordering requirement: a test must be no smaller than its preconditions. With these in hand, we’re able to automatically derive a KAT with good properties in a pay-as-you-go fashion:

  • If your theory is sound, the KAT is sound.
  • If your theory is complete, the KAT is complete.
  • If your theory’s satisfiability checking is decidable, we can derive a decision procedure for equivalence.

I’m particularly excited that our framework is prototype-ready: our code is implemented as an OCaml library, where you define theories as functors. Please try it out—mess around and write your own theories, following our examples. We hope that KMT will significantly lower the bar for entry, making it easier for more people to play around with KAT’s powerful equivalence checking.

What’s the catch?

There’s more than one way to cook a KAT. KMT generates KATs with tracing semantics, i.e., the exact trace of actions matters. In KAT+B! or NetKAT, later updates override earlier ones, e.g., x:=false; x:=true ? x:=true… but KMT will treat these terms differently, because they have different traces. KAT+B! deliberately avoids tracing; NetKAT only traces at predefined points, by means of their dup primitive, which marks the current state as historically salient. There’s no deep reason for KMT to use tracing, and we believe KMT can be generalized to support dup-like controls for tracing.

The ordering constraint on weakest preconditions is a strong one. Our natural numbers, sets, and maps must be monotonic: they may grow or shrink, but not both. They cannot be compared, e.g., two natural-valued variables x and y can be compared to constants but not each other.

KMT is also just a prototype. It’s fast for small programs, but it takes dedicated work to make a KAT’s decision procedure efficient enough on more serious examples.

Why are you talking about cooking KATs?

The greatest POPL paper of all time is Manna and Pnueli 1983, “How to cook a temporal proof system for your pet language”. Why? Just take a look a the first page:

The header of the paper offsets the author names to the right. A line drawing dominates the top: a dog wags its tail, tongue dripping eagerly in front of a kabob marked with "ADA" and "shared variable" and "CSP".
I rest my case.

Update

KMT won a distinguished paper award at PLDI!

Summarizing performance numbers

PapersLeave a comment

How should we summarize performance numbers? In a recent benchmark run, I had some interesting speedup numbers that I wasn’t certain how to report. While it’s easy to make charts that are illuminating, I’m not certain what I should say in, e.g., an abstract.

Here’s the raw data (also available as a spreadsheet), noting that I’ve made everything as abstract as I can:

In the data, I’ve recorded the runtime of 2 tools (tool1 and tool2) on 40 tests. The tests are lettered by theme, with a number to distinguish tests that are somehow related. Each runtime in the table is in seconds, and is the arithmetic mean of three runs exhibiting nominal variation. I run tool1 in two configurations: tool1 simply solves the problem, while tool1.min tries to solve the problem “minimally” in some sense. I run tool2 in only one configuration. In the spreadsheet, I’ve calculated a few summary statistics for each column. Here are the summary statistics for tool1 vs. tool2:

Min1.00
Arithmetic mean156.84
Geometric mean12.64
Harmonic mean4.49
Median7.57
Max3332.12
Summary statistics of tool1’s speedup compared to tool2

Doing some cursory analysis in R, it’s easy to generate charts that give a pretty good feel for the data. (It’s all in mgree/summarizing-perf on GitHub.) Here’s a box plot of times:

boxplots showing runtimes for tool1, tool1.min, and tool2. tool1 is the tightest, lowest box; tool1.min is a little higher but has the same median; tool2 is substantially higher (worse) than the other two.

And here’s a violin plot of times:

a violin plot shows that tool1 and tool1.min are chonkiest around 0.05s, while tool2 has wide variation

I would summarize these charts in text as, “tool1 is an order of magnitude faster than tool2; minimization closes some of the gap, but tool1.min is still substantially faster than tool2”. A bar chart tells the same story:

a bar chart comparing tool1, tool1.min, and tool2 across all tests. tool2 is only rarely competitive with tool1 (i.e., withing half an order of magnitude). tool1.min does worse than tool1, but still typically beats tool2.

With the bar chart, it’s possible to see that sometimes tool2 is in the same league as tool1, but not usually. We have tool2 beating tool1.min only once (test w); it never beats tool1, and typically loses by 1-2 orders of magnitude. Some cases are catastrophically bad.

Plotting speedup lets us justify some other comments. Here’s a scatter plot:

a scatter plot showing speedups for tool1 and tool1.min. a single point for tool1 is on the 1; all others are above. a single point for tool1.min is below the 1; all others are above.

And here’s a boxplot of speedups in aggregate:

a boxplot summarizing speedups of tool1 and tool1.min compared to tool2. the whisker for tool1 stops at 1; the whisker for tool2 goes just below. the medians and quartiles are more or less comparable, with tool1 doing a touch better than tool1.min

Looking at these speedups, I’d feel comfortable saying that “tool1 is typically an order of magnitude faster than tool2, never slower, and sometimes much faster; tool1.min behaves similarly, though it can sometimes be slower”.

This post comes out of a Twitter thread, which is a goldmine of insight and resources. Please check it out, and chime here or in the thread with your thoughts!

Special thanks to Noam Ross for help with some of the fancier log-scale stuff on the plots.

Bridging the gradual typing gap at OOPSLA 2021

Blog, Papers, Programming LanguagesLeave a comment

I want to believe in a future where the lion will lie down with the lamb; we’ll beat our swords into plowshares; and developers will migrate dynamic prototypes to robust static systems with confidence. But these Aquarian visions are elusive. Having a map of the road to paradise in theory doesn’t mean we know how to get there in practice. Let me tell you about two papers at OOPSLA that shuffle us a few steps forward on this long pilgrim’s trail.

A vintage poster of "Hair", the American Tribal Love Rock Musical, with a trippy inverted head. This poster advertises a performance at the Aquarius Theatre in Los angeles.

Migrating programs

How do you actually get a program from Scheme into ML? Or from JavaScript into TypeScript? The theory of gradual typing goes far beyond these pedestrian questions. In principle, we know how to reconcile dynamism with much more complex systems, like information flow or refinement types or effect systems. But there’s very little tooling to support moving any particular Scheme program into ML. (If your program is a Racket program, then you’re in some luck.)

People have studied program migration before, under a variety of names. Papers go back at least to 2009, arguably even earlier. There are lots of different approaches, and most comprise some form of type inference and custom constraint solving—complex! Worse still, there’s been no consensus on how to evaluate these systems. Luna Phipps-Costin, Carolyn Jane Anderson, me, and Arjun Guha dug into program migration. Our paper, “Solver-based Gradual Type Migration”, tries to build a map of the known territory so far:

  1. There are competing desiderata: maximal type precision, compatibility with code at different types, and preserving the existing semantics of your program, i.e., safety.
  2. We evaluate a variety of past techniques on prior benchmarks, and we devise a novel set of “challenge” problems. Our evaluation framework is robust, and you could plug in other approaches to type migration and evaluate them easily.
  3. We introduce a new, very simple approach to type migration, which we call TypeWhich. TypeWhich uses an off-the-shelf SMT solver. You can choose how compatible/precise you want it to be, but it’ll always be safe.

I’m excited about each of these contributions, each for its own reason.

For (1), I’m excited to formally explain that what you’re actually trying to do with your code matters. “Gradual typing” sensu lato is pretty latus indeed. Are you migrating a closed system, module by module? Or are you coming up with type annotations for a library that might well be called by untyped clients? These are very different scenarios, and you probably want your type migration algorithm to do different things! Bringing in these competing concerns—precision, compatibility, and safety—gives researchers a way to contextualize their approaches to type migration. (All that said, to me, safety is paramount. I’m not at all interested in a type migration that takes a dynamic program that runs correctly on some input and produces a statically typed program that fails on the same input… or won’t even compile! That doesn’t sound very gradual to me.)

For (2), I’m excited to be building a platform for other researchers. To be clear, there’s a long way to go. Our challenge problems are tiny toys. There’s a lot more to do here.

For (3), I’m excited to have an opportunity to simplify things. The TypeWhich constraint generator is simple, classic PL; the constraints it generates for SMT are straightforward; the models that SMT generates are easy to understand. It’s a cool approach!

One tiny final note: Luna has done a tremendous amount of incredibly high quality work on this project, both in code and concept. She’s just now starting her third-year of undergraduate study. So: watch out! You ain’t ready.

Typed functional programming isn’t about functions

If there’s a single defining ‘killer’ feature of typed functional programming, it isn’t first-class functions at all: it’s algebraic datatypes. Algebraic datatypes help make illegal states unrepresentable and ASTs easy to work with. They’re a powerful tool, and their uptake in a variety of new-hotness languages (Kotlin, Rust, Swift) speaks to their broad appeal.

Moving Scheme code to ML is an old goal, and it’s the bread and butter of the introductory sections of gradual typing papers. But are we any closer than we were fifteen years ago? (I’d say “yes”, and point at Typed Racket, or “nobody knows what’s happening anyway” and point at Idris’s Chez Scheme runtime.)

Stefan Malewski, me, and Éric Tanter tried to figure out how algebraic datatypes play with dynamic features. Our paper, “Gradually Structured Data“, uses AGT to ‘compute’ static and dynamic semantics for a language with possibly open algebraic datatypes and the unknown type in a few flavors (?, the unknown type; a new ground type for “datatype”, the same way int and bool and ?->? are ground; and a new type for “any open datatype”). The features gel in a nice way, letting us express some cool behaviors (see Section 2 for how one might evolve a simple JSON API) and sit in a novel space (see Section 5 for a thorough comparison to related features).

I’m particularly pleased that we’ve found a new place in the design spectrum (per our feature chart in Section 5) that seems to support incremental program migration (per our examples in Section 2)—and it’s formally grounded (by using AGT in the middle, formal sections).

This paper came out of conversations with Éric after my screed about gradual typing’s two lineages at SNAPL (see also my followup blogpost, “What to Define When You’re Defining Gradual Type Systems”). There’s plenty more to do: what about separate compilation? What are the right representation choices? How should runtime checks really go, and how can programmers control the costs?

I remember a question I was asked after giving the talk for “Contracts Made Manifest” at POPL 2010 with some panic fondly. That paper compares the latent approach to contracts in Racket-then-Scheme (well structured runtime checks at module boundaries) to the manifest approach (runtime checks are a form of type coercion, occurring anywhere) in the emerging refinement types literature (Sage, Liquid Types, etc.). I had shown that the two aren’t equivalent in the presence of dependency, and I concluded by talking about how the two implementation approaches differed. So: somebody asked, “Which approach should you use?” To be honest, I had hardly even thought about it.

So, suppose you wanted use algebraic datatypes and dynamic features today: which language should you use? I’ve thought about it, and the answer, sadly, is, “It depends”. OCaml’s polymorphic variants get you a long way; Haskell’s Dynamic could work great, but it’s badly in need of usable surface syntax. (I’ve tried to get Richard Eisenberg to help me with the fancy work to make that happen, but he’s justifiably worried that the Haskell community would run him out of town.) Scala, Haskell, and OCaml are your best bets if you want true algebraic datatypes. If you’re more relaxed about things, Typed Racket or TypeScript could work well for you. If what you’re looking for is a type system expressive enough to capture interesting dynamic idioms, then I think there’s a clear choice: CDuce. Ever since un bel recensore anonimo at SNAPL 2019 showed me that CDuce can type flatten, I’ve been impressed. Check this out:

let flatten ( Any -> [ (Any\[Any*])* ] )  (* returns a list of non-lists ???? *)
  | [] -> []                              (* nil *)
  | (h,t) -> (flatten h)@(flatten t)      (* cons *)
  | x -> [x]                              (* anything else *)

Look at that type! In just a few lines of CDuce, we can show that flatten produces not just a list of elements, but a list of things that are not themselves lists. The price here is that CDuce’s types are set-theoretic, which means things are a touch different from what people are used to in OCaml or Haskell. But if you’re okay with that, CDuce is a serious contender!

Coda: see you at OOPSLA?

I’m planning on going to OOPSLA 2021 in Chicago, given the twoopsla and the opportunity to present a paper from OOPSLA 2020, “Formulog: Datalog for SMT-based static analysis”, with Aaron Bembenek and Steve Chong. I’ve already blogged about it, but I’m excited to get to give an in-person version of the talk, too. You can still watch Aaron’s excellent recorded talk on YouTube and enjoy the cabin vibes. There won’t be cabin vibes at my OOPSLA 2020 talk, but there will be terrible jokes. So: think about it. Will I see you at OOPSLA? I hope so!

SIGPLAN Blog: Making PL Ideas Accessible

Blog, PapersLeave a comment

I have a new post up on the SIGPLAN blog: “Making PL Ideas Accessible: An Open-Source, Open-Access, Interactive Journal. Inspired by Distill, I propose an open-access, open-source, interactive journal for disseminating clear presentations of current ideas and methods in programming languages.

It’s a particularly good moment to consider our research’s reach and impact: CORE has just downgraded many PL conferences in its rankings. Just because you don’t take an interest in rankings doesn’t mean rankings won’t take an interest in you. Let this spur a new wave of beautiful and enlightening explanations of PL ideas that can reach a a broad audience.

Formulog: ML + Datalog + SMT

Blog, Papers, Programming Languages, Software3 Comments

If you read a description of a static analysis in a paper, what might you find? There’ll be some cute model of a language. Maybe some inference rules describing the analysis itself, but those rules probably rely on a variety of helper functions. These days, the analysis likely involves some logical reasoning: about the terms in the language, the branches conditionals might take, and so on.

What makes a language good for implementing such an analysis? You’d want a variety of features:

  • Algebraic data types to model the language AST.
  • Logic programming for cleanly specifying inference rules.
  • Pure functional code for writing the helper functions.
  • An SMT solver for answering logical queries.

Aaron Bembenek, Steve Chong, and I have developed a design that hits the sweet spot of those four points: given Datalog as a core, you add constructors, pure ML, and a type-safe interface to SMT. If you set things up just right, the system is a powerful and ergonomic way to write static analyses.

Formulog is our prototype implementation of our design; our paper on Formulog and its design was just conditionally accepted to OOPSLA 2020. To give a sense of why I’m excited, let me excerpt from our simple liquid type checker. Weighing in under 400 very short lines, it’s a nice showcase of how expressive Formulog is. (Our paper discusses substantially more complex examples.)

type base =
  | base_bool

type typ = 
  | typ_tvar(tvar)
  | typ_fun(var, typ, typ)
  | typ_forall(tvar, typ)
  | typ_ref(var, base, exp)

and exp = 
  | exp_var(var)
  | exp_bool(bool)
  | exp_op(op)
  | exp_lam(var, typ, exp)
  | exp_tlam(tvar, exp)
  | exp_app(exp, exp)
  | exp_tapp(exp, typ)

ADTs let you define your AST in a straightforward way. Here, bool is our only base type, but we could add more. Let’s look at some of the inference rules:

(* subtyping *)
output sub(ctx, typ, typ)

(* bidirectional typing rules *)
output synth(ctx, exp, typ)
output check(ctx, exp, typ)

(* subtyping between refinement types is implication *)
sub(G, typ_ref(X, B, E1), typ_ref(Y, B, E2)) :-
  wf_ctx(G),
  exp_subst(Y, exp_var(X), E2) = E2prime,
  encode_ctx(G, PhiG),
  encode_exp(E1, Phi1),
  encode_exp(E2prime, Phi2),
  is_valid(`PhiG /\ Phi1 ==> Phi2`).

(* lambda and application synth rules *)
synth(G, exp_lam(X, T1, E), T) :-
  wf_typ(G, T1),
  synth(ctx_var(G, X, T1), E, T2),
  typ_fun(X, T1, T2) = T.

synth(G, exp_app(E1, E2), T) :-
  synth(G, E1, typ_fun(X, T1, T2)),
  check(G, E2, T1),
  typ_subst(X, E2, T2) = T.

(* the only checking rule *)
check(G, E, T) :-
  synth(G, E, Tprime),
  sub(G, Tprime, T).

First, we declare our relations—that is, the (typed) inference rules we’ll be using. We show the most interesting case of subtyping: refinement implication. Several helper relations (wf_ctx, encode_*) and helper functions (exp_subst) patch things together. The typing rules below follow a similar pattern, mixing the synth and check bidirectional typing relations with calls to helper functions like typ_subst.

fun exp_subst(X: var, E : exp, Etgt : exp) : exp =
  match Etgt with
  | exp_var(Y) => if X = Y then E else Etgt
  | exp_bool(_) => Etgt
  | exp_op(_) => Etgt
  | exp_lam(Y, Tlam, Elam) =>
    let Yfresh = 
      fresh_for(Y, X::append(typ_freevars(Tlam), exp_freevars(Elam)))
    in
    let Elamfresh = 
      if Y = Yfresh
      then Elam
      else exp_subst(Y, exp_var(Yfresh), Elam)
    in
    exp_lam(Yfresh,
            typ_subst(X, E, Tlam),
            Elamfresh)
  | exp_tlam(A, Etlam) =>
    exp_tlam(A, exp_subst(X, E, Etlam))
  | exp_app(E1, E2) => 
    exp_app(exp_subst(X, E, E1), exp_subst(X, E, E2))
  | exp_tapp(Etapp, T) => 
    exp_tapp(exp_subst(X, E, Etapp), typ_subst(X, E, T))
  end

Expression substitution might be boring, but it shows the ML fragment well enough. It’s more or less the usual ML, though functions need to have pure interfaces, and we have a few restrictions in place to keep typing simple in our prototype.

There’s lots of fun stuff that doesn’t make it into this example: not only can relations call functions, but functions can examine relations (so long as everything is stratified). Hiding inside fresh_for is a clever approach to name generation that guarantees freshness… but is also deterministic and won’t interfere with parallel execution. The draft paper has more substantial examples.

We’re not the first to combine logic programming and SMT. What makes our design a sweet spot is that it doesn’t let SMT get in the way of Datalog’s straightforward and powerful execution model. Datalog execution is readily parallelizable; the magic sets transformation can turn Datalog’s exhaustive, bottom-up search into a goal-directed one. It’s not news that Datalog can turn these tricks—Yiannis Smaragdakis has been saying it for years!—but integrating Datalog cleanly with ML functions and SMT is new. Check out the draft paper for a detailed related work comparison. While our design is, in the end, not so complicated, getting there was hard.

Relatedly, we have also have an extended abstract at ICLP 2020, detailing some experiments in using incremental solving modes from Formulog. You might worry that Datalog’s BFS (or heuristic) strategy wouldn’t work with an SMT solver’s push/pop (i.e., DFS) assertion stack—but a few implementation tricks and check-sat-assuming indeed provide speedups.

Flapjax on PL Perspectives

Blog, Flapjax, JavaScript, Papers, Programming LanguagesLeave a comment

Shriram Krishnamurthi, Arjun Guha, Leo Meyerovich, and I wrote a post about Flapjax on PL Perspectives, the SIGPLAN blog. (Thanks to Mike Hicks for helping us edit the post!)

Flapjax won the OOPSLA MIP award for 2009 (though the SIGPLAN website isn’t yet up to date). Our blog post is about the slightly unconventional way we worked: most of the Flapjax work happened in 2006 and 2007, but we didn’t even try to write the paper until several years later (Leo and I were in grad school). Rather than recapitulate those ideas, go read the post!

Collapsible Contracts: Space-Efficient Contracts in Racket

Papers, Programming Languages1 Comment

While on sabbatical in Cambridge, MA (thanks, Steve!), I had the good fortune to attend my first SPLASH.

I was particularly excited by one paper: Collapsible Contracts: Fixing a Pathology of Gradual Typing by Daniel Feltey, Ben Greenman, Christophe Scholliers, Robby Findler, and Vincent St-Amour. (You can get the PDF from the ACM DL or from Vincent’s website.)

Their collapsible contracts are an implementation of the theory in my papers on space-efficient contracts (Space-Efficient Manifest Contracts from POPL 2015 and Space-Efficient Latent Contracts from TFP 2016). They use my merge algorithm to ‘collapse’ contracts and reduce some pathologically bad overheads. I’m delighted that my theory works with only a few bits of engineering cleverness:

  • Racket’s contracts are first-class values, which means subtle implementation details can impede detecting duplicates. Racket’s contract-stronger? seems to do a good enough job—though it helps that many contracts in Racket are just checking simple types.
  • There’s an overhead to using the merge strategy in both space and time. You don’t want to pay the price on every contract, but only for those that would consume unbounded space. Their implementation waits until something has been wrapped ten times before using the space-efficient algorithms.
  • Implication queries can be expensive; they memoize the results of merges.

I am particularly pleased to see the theory/engineering–model/implementation cycle work on such a tight schedule. Very nice!

New paper: Word expansion supports POSIX shell interactivity

Papers, POSIX shell1 Comment

I’ve been thinking about and working on the POSIX shell for a little bit over a year now. I wrote a paper for OBT 2017, titled Understanding the POSIX Shell as a Programming Language, outlining why I think the shell is worthy of study.

For some time I’ve had the conviction that word expansion—the process that includes globbing with * but also things like command substitution with backticks—is somehow central to the shell’s interactivity. I’m pleased to have finally expressed my conviction in more detail: Word expansion supports POSIX shell interactivity will appear at PX 2018. Here’s the abstract:

The POSIX shell is the standard tool to deploy, control, and maintain systems of all kinds; the shell is used on a sliding scale from one-off commands in an interactive mode all the way to complex scripts managing, e.g., system boot sequences. For all of its utility, the POSIX shell is feared and maligned as a programming language: the shell is feared because of its incredible power, where a single command can destroy not just local but also remote systems; the shell is maligned because its semantics are non-standard, using word expansion where other languages would use evaluation.

I conjecture that word expansion is in fact an essential piece of the POSIX shell’s interactivity; word expansion is well adapted to the shell’s use cases and contributes critically to the shell’s interactive feel.

See you in Nice?

Space-Efficient Manifest Contracts at POPL 15

Papers, Programming LanguagesLeave a comment

I am delighted to announce that Space-Efficient Manifest Contracts will appear at POPL 2015 in Mumbai. Here’s the abstract:

The standard algorithm for higher-order contract checking can lead to unbounded space consumption and can destroy tail recursion, altering a program’s asymptotic space complexity. While space efficiency for gradual types—contracts mediating untyped and typed code—is well studied, sound space efficiency for manifest contracts—contracts that check stronger properties than simple types, e.g., “is a natural” instead of “is an integer”—remains an open problem.

We show how to achieve sound space efficiency for manifest contracts with strong predicate contracts. The essential trick is breaking the contract checking down into coercions: structured, blame-annotated lists of checks. By carefully preventing duplicate coercions from appearing, we can restore space efficiency while keeping the same observable behavior.

The conference version is a slightly cut down version of my submission, focusing on the main result: eidetic λH is a space-efficient manifest contract calculus with the same operational behavior as classic λH. More discussion and intermediate results—all in a unified framework for space efficiency—can be found in the technical report on the arXiv.